Article | 22/11/2011
Détermination de l'altitude des montagnes par la méthode géodésique
22/11/2011
Résumé
Dans cet article, nous présentons la détermination de l'altitude d'une montagne par une méthode géodésique simplifiée, mise en œuvre par quatre élèves (Arthur, Dimitri, François-Xavier et Lucas) de première scientifique dans le cadre d'un atelier scientifique. La méthode est exigeante et fournit un formidable apprentissage de la démarche scientifique : reconnaissance préalable sur le terrain pour trouver des stations de visée pertinentes, nécessité de mesures précises, de corrections multiples (corrections de sphéricité et de réfraction) et de calculs trigonométriques abordables mais délicats.
Table des matières
Introduction
L'altitude d'un point est la distance, mesurée selon la verticale du lieu, qui sépare ce point d'une surface de référence appelée géoïde. Le géoïde est la surface moyenne des océans, prolongée par la pensée sous les continents. Comment déterminer l'altitude d'une montagne ? La réponse est moins simple qu'il n'y paraît de prime abord. Nous explorerons ici la méthode du nivellement trigonométrique ou géodésique, qui ne détermine pas directement l'altitude de la montagne mais la différence d'altitude entre le sommet et un point de référence, d'altitude connue. Cette méthode ne nécessite pas l'ascension de la montagne. Il s'agit d'effectuer des visées du sommet depuis deux points de la plaine dont on connaît l'éloignement et l'altitude. La mesure des angles et d'une distance permet, à l'aide de formules trigonométriques, de déterminer la différence d'altitudes entre le sommet et les deux points de la plaine.
Cette méthode a été mise en œuvre par 4 élèves du lycée Jean Monnet d'Annemasse, pour déterminer l'altitude du Môle (Haute Savoie), sommet proche, situé à environ 15 km au Sud-Est d'Annemasse.
Principe de la méthode géodésique
Quelle(s) visée(s) effectuer ?
Première idée
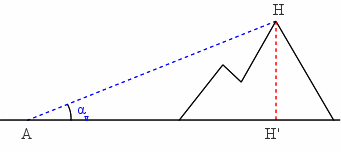
Pour déterminer l'altitude d'une montagne, ou plutôt la différence de hauteur entre le sommet H de la montagne et un point A de la plaine, une première idée pourrait être de mesurer la hauteur angulaire αv du sommet depuis le point A. La hauteur HH' est donnée par : HH' = tan(αv) x AH' ou HH' = sin(αv) x AH. Les distances AH' et AH ne sont cependant pas connues ! La distance AH' n'est jamais mesurable directement et AH est une distance souvent trop grande pour être mesurée par les appareils courants.
Deuxième idée
Pour contourner la difficulté et déterminer la distance AH, l'idée est de mesurer des angles et une autre distance accessible, puis d'en déduire la première par un calcul de trigonométrie.
Soit un triangle quelconque ABC, posons que le côté c et les deux angles α et β qui le bordent sont connus.
D'après la loi des sinus : a/sin(α) = b/sin(β) = c/sin(γ). Or γ = π- (α+β), et donc, sin(γ) = sin(α+β).
Les côtés a et b peuvent donc s'exprimer à partir de c, α et β :
- a = c.sin(α) / sin(α+β)
- b = c.sin(β) / sin(α+β)
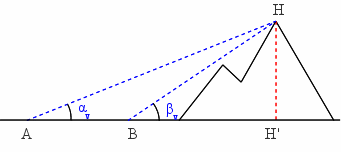
En conclusion, si l'on connaît un côté du triangle et deux angles, tous les côtés peuvent être déterminés. Il s'agit donc de mesurer la hauteur angulaire du sommet H depuis deux points différents de la plaine A et B, ainsi que leur éloignement AB. A et B sont à la même altitude et sont choisis de telle sorte qu'ils sont alignés avec le sommet H.
Les formules de trigonométrie appliquées au triangle ABH permettent de calculer AH (attention, l'angle β des formules générales correspond ici à π-βv) :
- AH = AB.sin(βv) / sin(βv-αv).
HH' s'en déduit alors aisément : .HH' = sin(αv.AH)
La méthode est simple et élégante. Même si A et B ne sont pas à la même altitude, le calcul de HH' peut être effectué par une méthode similaire. Mais sur le terrain, il est contraignant de trouver deux points de mesure visibles entre eux et alignés avec le sommet à viser.
Troisième idée
Une autre méthode s'impose. Il s'agit toujours de viser le sommet H de la montagne depuis deux points différents A et B de la plaine dont l'éloignement AB est connu, mais cette fois les points A et B ne sont pas alignés avec le sommet. Deux séries de mesures successives sont nécessaires : la première dans le plan horizontal de la station A et la deuxième dans le plan vertical passant par la station A et le sommet H.
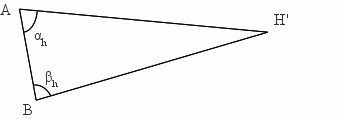
Les visées dans le plan horizontal permettent de calculer la distance horizontale AH' (figure ci-dessous) :
- AH' = AB.sin(βh) / sin(αh+βh).
Figure 3. Visée du sommet dans le plan horizontal de la station A
C'est le point H' qui est le troisième terme du triangle et non H.
Puisque AH' a été déterminée, HH' peut être calculée en faisant la visée du sommet dans le plan vertical (Figure 1) : HH' = tan(αv) x AH'. Cette méthode est plus souple que la précédente puisque les points A et B peuvent être choisis plus librement en fonction des contraintes du terrain. Elle nécessite la mesure d'une distance (AB), de deux angles horizontaux (αh et βh) et d'un angle vertical (αv). Mais rien n'empêche de faire avec le point B ce qui a été fait avec le point A. Donc en mesurant en plus βv, on peut avoir également une deuxième détermination de la hauteur du sommet H par rapport au point B.
Les corrections
Les visées ne peuvent pas être exploitées directement ; elles doivent être corrigées de deux facteurs : la sphéricité de la Terre et la réfraction atmosphérique.
La sphéricité de la Terre
La Terre n'est pas plate ! Lorsque l'on détermine la hauteur d'une montagne par rapport à un plan horizontal passant par la station de visée, on effectue une erreur.
Figure 4. L'effet de la sphéricité de la Terre
O designe le centre de la Terre, supposée sphérique.
La triangulation donne accès à la hauteur H'H mais le point H' n'est pas à la même altitude que le point A. Pour pouvoir déterminer la différence de hauteur entre H et A, il faut connaître DH. La correction due à la sphéricité de la Terre est donc Cs = DH'. Elle est positive. Comme les distances impliquées dans la triangulation géodésique sont petites par rapport au rayon de la Terre (RT), on peut toujours supposer que le triangle AH'H est rectangle en H'. En utilisant le théorème de Pythagore dans le triangle OAH', rectangle en A, donc d'hypothénuse OH', on a :
- RT2 + AH'2 = (RT+DH')2 ,
- soit encore : AH'2 = 2RT x DH' + DH'2.
Comme DH'2 est négligeable devant les autres termes, on a finalement :
- Cs = DH' = AH'2 / 2RT.
La correction de sphéricité augmente avec le carré de la distance entre les deux points de visée.
Quelques exemples, avec RT = 6370 km :
- Cs = 1,96 cm pour AH' = 500 m ;
- Cs = 1,96 m pour AH' = 5 km ;
- Cs = 7,85 m pour AH' = 10 km.
La réfraction atmosphérique
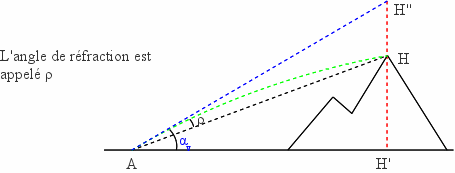
Lors de la visée du sommet, le rayon lumineux ne suit pas une ligne droite mais une ligne courbe (figure ci-dessous). La courbure de la trajectoire n'est jamais identique, elle varie non seulement tous les jours mais à toutes les heures de la journée. La position apparente H'' du sommet que l'on vise change donc à chaque instant suivant l'état de l'atmosphère. Ces phénomènes proviennent de la réfraction atmosphérique et doivent être corrigés. Disons-le d'emblée, ces corrections sont très imparfaites et ce sont elles qui limitent la précision des visées géodésiques.
Figure 5. L'effet de la réfraction atmosphérique
Le rayon lumineux (en vert) est courbe sa tangente au point A est dirigée vers H'', image du sommet H de la montagne. L'angle de réfraction est appelé ρ.
Les observations géodésiques montrent que l'angle de réfraction ρ présente un certain nombre de caractéristiques. Il est maximum la nuit, décroît au lever du jour, atteint un minimum vers 10h solaire (en été), reste plus au moins constant jusqu'à 15h solaire, et recroît ensuite. La valeur de l'angle minimum est assez régulière en été : elle se reproduit à peu près identique à elle-même les jours ou les conditions météorologiques sont semblables. On constate également que l'angle de réfraction ρ observé pendant le temps du minimum de réfraction est sensiblement proportionnel à la longueur du côté mesuré divisée par le rayon de la Terre :
- ρ = K x AH'/RT ; avec K ≈ 0,065 et ρ en radians.
Pour estimer la correction Cr = HH'', on peut calculer la distance verticale résultant de l'angle ρ lorsque l'on est placé en H'.
Comme ρ est petit, on a :
- ρ ≈tan(ρ) = Cr / AH' , donc Cr = ρ x AH' = K x AH'2/ RT.
En comparant avec la correction de sphéricité, on obtient : Cr = 2.K.Cs , soit Cr ≈ Cs / 8.
La correction due à la réfraction est environ huit fois plus petite que celle due à la sphéricité. Mais leurs signes sont opposés. La réfraction relève les objets et, du coup, ils apparaissent plus grands qu'ils ne le sont en réalité. La valeur de cette correction n'est qu'une estimation. Elle s'approche le plus de la réalité les jours d'été lorsque la visée a été effectuée entre 10h et 15h solaire.
Application : mesure de l'altitude du Môle
La méthode précédente a été utilisée pour la détermination de l'altitude du Môle. Ce sommet, situé à seulement 15 km au Sud-Est d'Annemasse dans la vallée de l'Arve, a été choisi en raison de la présence d'une croix à son sommet, que l'on peut viser facilement. La réalisation des mesures n'a été possible que grâce à l'aide de M. Gilbert Meynet, topographe de métier. L'appareil utilisé est un tachéomètre, qui permet des mesures de distance (de l'ordre de 300 m) et des mesures d'angles à travers une lunette qui agrandit 30 fois.
Choix des points de mesure
L'opération se déroule dans la vallée de l'Arve, entre Fessy (74800), près d'Arenthon, et Saint Laurent (figures ci-dessous). Les stations sont visibles entre elles et permettent de viser le Môle. La station Fessy1 est une borne géodésique de l'IGN, d'altitude parfaitement connue, qui est notre référence des altitudes (445,4 m). La station de Saint Laurent est également une borne géodésique, ce qui nous permettra de vérifier les calculs de la première triangulation.
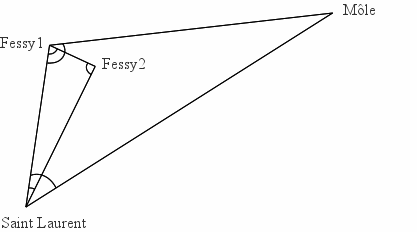
Figure 7. Plan des différentes stations de visées
Les cinq angles horizontaux mesurés sont indiqués.
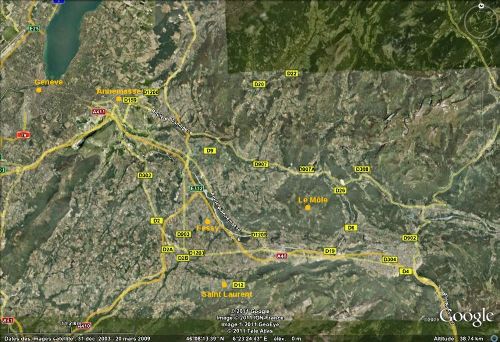
Figure 8. Localisation des sites de mesure.
Le tachéomètre utilisé ne permet que des mesures de faible distance (300 m), ce qui n'est pas suffisant pour effectuer une triangulation directe et précise avec le Môle. Nous avons donc réalisé deux triangulations successives. La première a pour but d'agrandir la base de départ. À partir de la mesure directe de la distance Fessy1-Fessy2 et la mesure des angles, nous avons calculé la distance Fessy1-Saint Laurent et l'altitude de Saint-Laurent. Puis la deuxième triangulation nous a permis de déterminer l'altitude du Môle en s'appuyant sur la base Fessy1-Saint Laurent. Au final, nous avons mesuré une distance, cinq angles horizontaux et six angles verticaux.
Les mesures
Pour obtenir une base de départ Fessy1-Fessy2 supérieure à 300 m (limite de l'appareil), nous avons placé le tachéomètre entre les deux stations et deux visées successives ont été réalisées en retournant l'appareil, d'abord vers Fessy1 puis vers Fessy2. Ces premières visées ont également servi à déterminer la hauteur de Fessy2 par rapport à Fessy1.
Pour la première triangulation, la hauteur du tachéomètre n'intervient pas puisque les visées ont été effectuées par rapport à un prisme, qui était toujours réglé à la même hauteur que le tachéomètre. Ce n'est plus le cas pour la deuxième triangulation, où c'était le centre de la croix du Môle qui était visé. La hauteur du tachéomètre doit alors être prise en compte et ajoutée au résultat final.
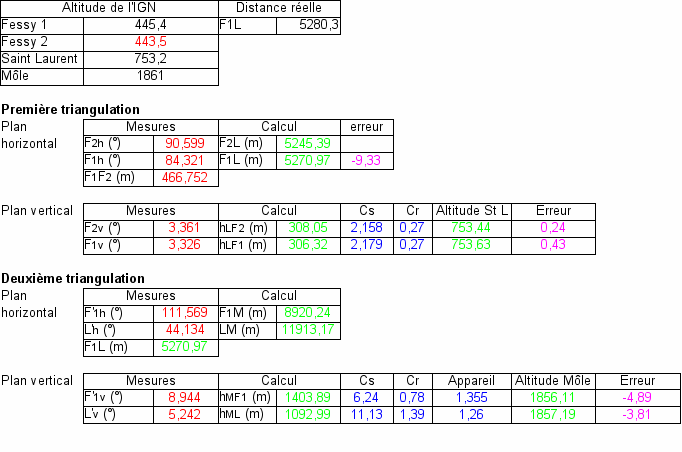
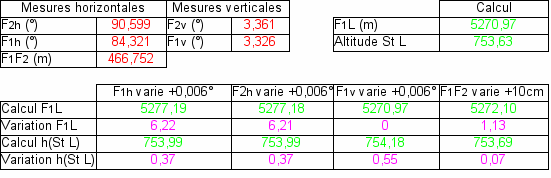
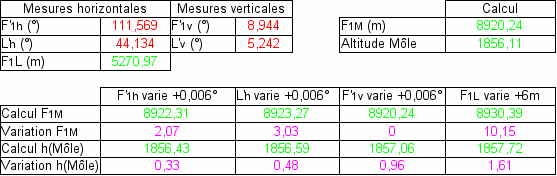
Dans le tableau ci-dessous, nous donnons nos mesures et nos calculs. La distance réelle entre Fessy1 et Saint-Laurent, qui correspondaient à des bornes géodésiques de l'IGN, a été calculée avec les outils de Google maps.
Tableau 1. Altitude du Môle : mesures (en rouge), calculs (en vert), corrections (en bleu) et erreurs (en violet) par rapport aux déterminations de l'IGN (en noir)
Discussion sur l'origine des erreurs
Lors de la première triangulation, les trois angles horizontaux du triangle ont été mesurés et leur somme était de 179,982°. Sur l'ensemble des trois mesures, l'erreur commise était donc de 0,018°, ce qui fait en moyenne une erreur de 0,006° = 0,36' sur chaque angle. Comme dans cette première triangulation les distances sont de l'ordre de 5000 m, cette erreur dans la mesure de l'angle résulte d'une erreur dans le positionnement de (tan(0,006) x 5000 m, soit O,5 m..
Cette erreur ne paraît pas aberrante. En effet, le jour où nous avons fait les mesures, la luminosité était médiocre. Malgré la lunette du tachéomètre qui agrandit 30 fois, nous avions du mal à réaliser les visées. Pour remédier à cette difficulté, il aurait fallut disposer d'une source de lumière puissante, qui aurait été un point beaucoup plus facile à viser.
Sensibilité des mesures pour l'altitude de Saint Laurent (première triangulation)
Dans le tableau ci-dessous, nous cherchons quelle est la conséquence sur la précision des résultats de cette erreur dans les angles de 0,006° (nous supposons que cette erreur est la même pour les angles horizontaux et verticaux). Nous regardons également quel est l'effet d'une petite erreur (de l'ordre de la dizaine de cm) dans la mesure de la base de départ (cette erreur peut par exemple provenir de la difficulté de tenir le prisme parfaitement à la verticale).
Nous voyons que, sans tenir compte de la réfraction, nos mesures donnent une valeur de l'altitude de Saint Laurent au mètre près (somme des variations h(St L)).
Sensibilité des mesures pour l'altitude du Môle (seconde triangulation)
La variation de la base F1L de +6 m correspond à la valeur obtenue précédemment. Sans tenir compte de la réfraction, notre mesure donne une valeur de l'altitude du Môle à 3 mètres près.
Il est difficile de quantifier les erreurs sur la correction de la réfraction atmosphérique. La valeur de Cr ≈ Cs/8 n'est valable que les jours d'été lorsque la visée est effectuée entre 10h et 15h solaire, ce qui est tout sauf notre cas ! Il est peu probable que notre prise en compte de la réfraction soit juste...
Pour aller plus loin
La réfraction atmosphérique rend les visées géodésiques délicates. Ainsi une méthode plus précise a été développée pour déterminer l'altitude d'une montagne. Elle consiste à effectuer des visées réciproques et simultanées depuis la station en plaine et depuis le sommet de la montagne. C'est-à-dire qu'un appareil est monté au sommet de la montagne et que si le sommet est visé depuis la plaine, la station en plaine est également visée depuis la montagne. Cette réciprocité permet d'éliminer l'influence de la réfraction, en faisant l'hypothèse qu'elle est identique pour les deux visées.
Nous donnons uniquement la méthode, que l'on trouve dans les manuels de géodésie, sans l'avoir utilisée, faute de disposer de deux instruments de mesure.
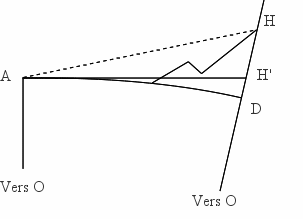
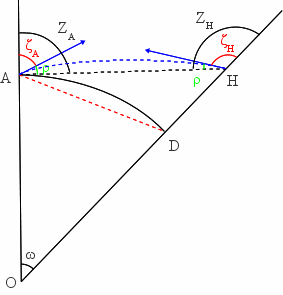
Figure 9. Visées réciproques et simultanées de la station A en plaine et du sommet H de la montagne
Le point D est la base de la montagne, située à la même altitude que A (les points A et D sont à la même distance du centre O de la Terre). Les visées ne suivent pas une ligne droite mais une ligne courbe. La mesure des distances zénithales permet de connaître ζA et ζH. Pour avoir les distances zénithales vraie ZA et ZH, il faut ajouter l'angle de réfraction ρ. On a donc : ZA = ζA + ρ, et ZH = ζH + ρ .
- Détermination de la distance AD.
Si la latitude et la longitude (φA et λA) du point A et (φD et λD) du point D sont connues, l'arc ω du grand cercle passant par ces deux points peut être déterminé grâce aux relations de trigonométrie sphérique (ω est en radians) :
- ω = acos[sin(φA).sin(φD) + cos(φA).cos(φD).cos(λD-λA)].
Comme le triangle OAD est isocèle, la longueur du segment AD est alors donné par :
- AD = 2.RT.sin(ω/2).
- Détermination de la hauteur de la montagne DH.
Il s'agit de déterminer la différence de hauteur DH, connaissant la distance AD et en mesurant les distances zénithales ζA et ζH.
Dans le triangle AOH la loi des sinus permet d'écrire :
- OH / sin(π-ZA) = OA / sin((π-ZH) ; soit encore OH / sin(ZA) = OA / sin(ZH).
Or, lorsqu'on a A/B=C/D, on a aussi (A-C)/(B-D)=(A+C)/(B+D).
On peut donc écrire :
- [OH-OA]/[sin(ZA)-sin(ZH)] = [OH+OA]/[sin(ZA)+sin(ZH)] ;
- ou encore, [OH-OA]/[OH+OA] = [sin(ZA)-sin(ZH)]/[sin(ZA)+sin(ZH)].
En utilisant les règles trigonométriques suivantes :
- sin[A] - sin[B] = sin[(A-B)/2] x cos[(A+B)/2] ;
- sin[A] + sin[B] = cos[(A-B)/2] x sin[(A+B)/2].
On obtient alors :
- [OH-OA]/[OH+OA] = ( sin[(ZA-ZH)/2] x cos[(ZA+ZH)/2] ) / ( cos[(ZA-ZH)/2] x sin[(ZA+ZH)/2] ) ;
- soit encore : [OH-OA]/[OH+OA] = tan[(ZA-ZH)/2] / tan[(ZA+ZH)/2].
Dans cette dernière expression, on peut remplacer certains termes :
- OH - OA = DH , puisque OA=OD ;
- OH + OA = 2RT + DH ≈ 2RT , puisque DH est négligeable devant RT ;
- ZA - ZH = ζA - ζH , puisque l'angle de réfraction est supposé identique depuis les deux points de visée ;
- ZA + ZH = π + ω , puisque la somme des angles est égale à π, dans le triangle AOH.
On obtient alors :
- DH / 2RT = tan[(ζA - ζH)/2] / tan[(π + ω)/2] ;
- soit encore, comme 1 / tan(A + π/2) = tan(A) : DH = 2RT x tan[ω)/2] x tan[(ζA - ζH)/2].
Or, en géodésie, ω reste très petit, donc tan(ω/2)≈sin(ω/2), ce qui permet d'écrire 2RT x tan[ω)/2] ≈ 2RT x sin[ω)/2] = AD.
Finalement, on a la relation : DH = AD x tan[(ζA - ζH)/2].
Pour déterminer la différence de hauteur entre le sommet d'une montagne et une station en plaine, il "suffit" de connaître les coordonnées géographiques de la station et de la montagne et de mesurer les distances zénithales ζA et ζH. La réfraction atmosphérique n'intervient pas ; elle disparaît lorsque l'on fait l'hypothèse qu'elle est identique pour les deux visée (depuis la plaine et depuis le sommet de la montagne).
Conclusion
La détermination de l'altitude d'une montagne par triangulation géodésique est un beau problème. La méthode simplifiée que nous avons mise en œuvre consiste à mesurer une distance accessible et des angles pour en déduire une distance inaccessible. Elle nécessite une reconnaissance préalable sur le terrain pour trouver des stations de visée pertinentes (visibles entres elles), des mesures précises et la prise en compte de corrections multiples (sphéricité et réfraction). La précision obtenue est moyenne (de l'ordre de 3 mètres) du fait de la difficulté d'effectuer des visées précises. Lorsqu'elle est réalisée par des professionnels, cette méthode offre une précision de l'ordre de quelques décimètres. Le procédé est cependant différent puisqu'il consiste à effectuer des visées réciproques et simultanées dans le plan vertical. Une autre méthode, appelée nivellement géométrique ou de précision, offre une précision encore plus grande. Elle n'est toutefois possible que le long des voies de communications. À l'aide d'un niveau à lunette dont l'axe optique est horizontal, deux mires graduées verticales identiques sont visées successivement, l'une située sur un point d'altitude connue, l'autre sur le point à déterminer : la différence de lecture donne la différence d'altitude. L'opération se poursuit de proche en proche, par cheminement, les portées ne dépassant jamais 30 ou 40 mètres. La précisions sur la différence d'altitude entre deux points distants de 500 km atteint alors le centimètre !
L'avènement de la géodésie spatiale révolutionne aujourd'hui la détermination des altitudes. Les systèmes de positionnement par satellite évitent les contraintes de la géodésie terrestre, tel que l'intervisibilité entre les points de mesure et l'impossibilité de faire des réseaux continentaux à grande échelle. Leur mise en œuvre sur le terrain est donc plus simple que les méthodes terrestres et ils permettent d'obtenir directement des coordonnées géométriques tridimensionnelles. notons toutefois que cela nécessite d'accéder physiquement au point dont on veut connaître l'altitude (les coordonnées). Par triangulation, l'altitude de l'Everest fut déterminée avant son ascension en 1953 (sans GPS, bien sûr). Les précisions obtenues aujourd'hui en géodésie spatiale (en absolu, meilleures que le centimètre) permettent aux scientifiques de suivre les évolutions temporelles : déplacement des plaques tectoniques pour les géophysiciens, surveillance des volcans pour les volcanologues, amélioration de la détermination du niveau moyen des mers pour les océanographes, etc. Aujourd'hui, il est possible d'obtenir des cartes topographiques par altmétrie satellite sans avoir besoin de se rendre sur place, malgré une moindre précision, ceci est très utile pour les endroits difficiles d'accès : zones de conflits, mais aussi Vénus ou Mars.